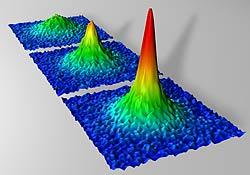
unitary Fermi gas
The core of an nuclei or the crust of a neutron star could be quantum simulated using cold atoms with Feshbach resonance. Image from NIST/JILA.
Introduction
Unitary Fermi gas models two component Fermi gas with infinite s-wave inter-specious scattering length. Considering relatively low temperature, because of the dominance of s-wave interaction, we could typically ignore p-wave interactions, etc. Another equivalent point of view is to consider them as identical fermions with an internal spin degree of freedom. Fermion could not flip spin during collision. If we label them as spin up and spin down. The two are equivalent, we could even rotate the spin up and spin down in a bloch sphere without changing the Hamiltonian. Thus we could alternatively call it SU(2) Fermi gas.
Unitary Fermi gas in nuclear and astrophysics
The crust of neutron star or the core of an nuclei

could be approximated by the unitary Fermi gas.
Scale invariance
Consider a homogeneous system with no external potential, the only length the system could possess is from the interaction. In the low temperature, the s-wave interaction could be described by the scattering length and effective range. In the extreme low temperature or dilute limit, we could even drop the effective range. This system has two special point, zero scattering length, which corresponds to non-interacting systems, and infinite scattering length, which corresponds to the unitary Fermi gas. At these two limits, the system is scale invariant. This means that, if you dilate or shrink the system, one simply need to multiply a scaling factor to the original Hamiltonian.
Atomic physics: Feshbach resonance
We could use Feshbach resonance to tune the scattering length of cold atoms from a weakly interacting system to unitary Fermi gas. For example, the ground \(^2\)S\(_{1/2}\) state of \(^6\)Lit has 6 hyperfine states.
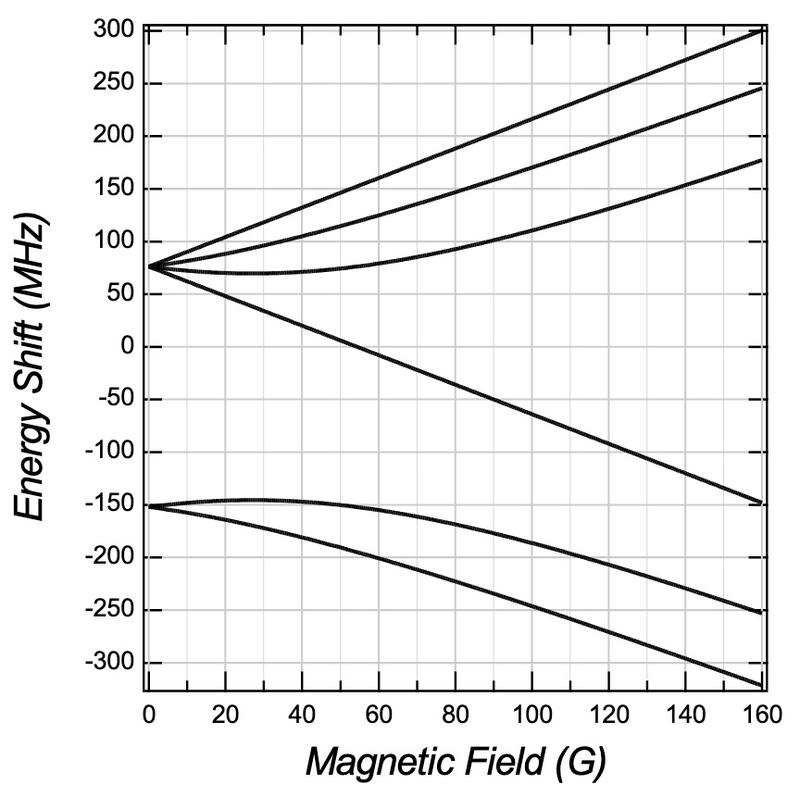
Picking up two of them, and tuning the magnetic fields to some magic number, the scattering length could be tuned to infinity.
Thermodynamics
We consider a grand canonical ensemble where the chemical potential is fixed. The equation of state of the unitary Fermi gas could be obtained consider a high temperature expansion. The expansion is called Virial expansion. Please see X.-J. Liu, Phys. Rep. 524, 37 (2013) for a review.
The expansion coefficients are called Virial coefficients.
Fourth order virial coefficients
We used the Path integral Monte Carlo(PIMC) method to determine the fourth-order Virial coefficient The figure below shows the virial coefficient as a function of inverse temperature in a harmonic trap.
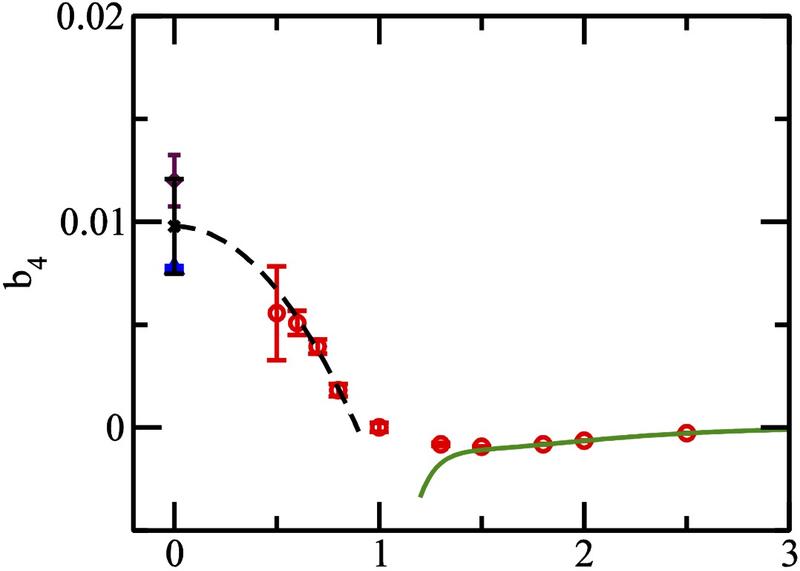
At low temperature, the coefficient is known to be negative (green). At high temperature, the coefficient is fitted from experiments to be positive. PIMC successfully calculated the virial coefficients in the intermiddiate temperature regime and show that there are no conflicts between theory and experiment.